We continue the course cs50, week three, sorting algorithms. It’s time for the lab. It is very simple:
- download test setup: https://cdn.cs50.net/2021/fall/labs/3/sort.zip
- inside the archive there are three already compiled C programs: sort1, sort2 and sort3 are binaries, i.e. binary code files, so we can’t view their C source code.
- each of these programs works on one of the sorting algorithms: selection sort, bubble sort, or merge sort. In what file what – we do not know. Our task is to determine which sorting algorithm is used in each binary..
In this task, you need to understand which program uses which algorithm, and you need to do this regardless of the program code itself, since it is not visible, but only by the time it takes to sort different data arrays. To do this, we are given several .txt files that contain numbers – there are three types of files:
- already sorted correctly;
- random order;
- sorted in reverse order.
The files have from 5 to 50 thousand values, and we can run each of the three programs for each of these 9 files with numbers, the launch of the sort program goes through the command line: ./[program_name] [text_file.txt]
For example, a run might look like this:
./sort1 reversed50000.txt.
To find out how long it will take the program to sort, start the timer through the terminal:
time ./[program_name] [text_file.txt].
We write down the real time value for ourselves, and use this data to analyze the algorithms. To pass the laboratory work, you need to fill in the answer.txt text file – write which program uses which algorithm and explain why you made such a conclusion. There is no need to write the code of the algorithms itself or to program anything at all. The task is reduced to analysis and logical search for an answer.
Shtukensia
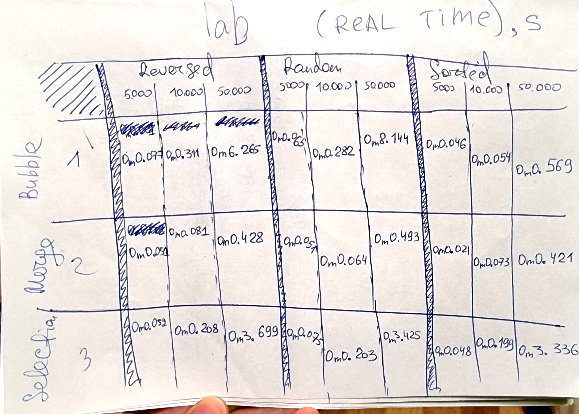
To complete this lab, I drew a table and filled it with data.:
Since we don’t have any data other than the sorting execution time, we need to look at the time and analytically guess which algorithm is which. Given that different algorithms have different minimum and maximum times, I initially focused on comparing the data from the first column (reversed) and the last column (sorted): these are our worst and best cases. Worst, since all data is sorted backwards. And the best, since all the numbers are in the right order anyway.
First, I found those two algorithms where the worst and best cases differ little, since their execution time is close (selection and merge), then from there I found an algorithm that becomes noticeably slower as the number of the reverse sorted array increases (bubble). Further, how to distinguish selection from merge? Merge sorts faster than select when increasing the amount of data. In the end, I compared how the algorithm behaves in general, even if the numbers are random. As a result, at first I found a bubble, and then I selected merge from the remaining two.
sort1 uses: bubble sort How do you know?: reversed and sorted speed soring is different (as n^2 and n) and for the biggest random list it is the slowest sort2 uses: merge sort How do you know?: it has the same or close sorting speed for best and worst cases and it much faster than 3rd (as nlogn) sort3 uses: selection sort How do you know?: it has the same or close sorting speed for reversed and sorted lists, but it become slower with growing of numbers (as n^2)
igroglaz
Well, I used a no less archaic way – a notepad 🙂 The following results were obtained:
sort 1 - slowest on random and reversed, but good at sorted bubble sort random 5000 .092 random 10000 .254 random 50000 8.145 reversed 5000 .089 reversed 10000 .285 reversed 50000 6.362 sorted 5000 .027 sorted 10000 .087 sorted 50000 .552 -- sort 2 - faster than any other for all types of data merge sort random 5000 .041 random 10000 .266 random 50000 .486 reversed 5000 .038 reversed 10000 .083 reversed 50000 .562 sorted 5000 .044 sorted 10000 .069 sorted 50000 .506 -- sort 3 - equal on any type of data selection sort random 5000 .070 random 10000 .179 random 50000 3.790 reversed 5000 .076 reversed 10000 .206 reversed 50000 3.744 sorted 5000 .047 sorted 10000 .172 sorted 50000 3.465
See you on new labs!